» HIRNFLIMMERN « ZURÜCK

Komprimierung

Durch Umwandlung mittels verschiedener Verfahren werden Daten in eine kürzere Form gebracht. Diese komprimierten Daten lassen sich durch Dekomprimierung wieder rekonstruieren.

Komprimierung ist grundsätzlich verlustfrei! Es werden ausschließlich redundante Informationen reduziert. Die in der Datei enthaltene Information bleibt erhalten.

(red|un|dant)
(<lat.> redundare – im Überfluss vorhanden sein, überreichlich)

Datenreduktion

Durch entfernen der Redundanzen und informationstragender Datenbereiche wird der Informationsgehaltes einer Datei verkleinert und somit auch die Datei selbst.

Aus durch Datenreduktion gewonnenen Dateien kann die ursprüngliche Datei nicht mehr rekonstruiert werden. Die reduzierten Informationen sind endgültig verloren.

LZW - Komprimierung

LZW ist ein nach Abraham Lempel, Jakob Ziv und Terry A. Welch benanntes verlustfreies Komprimierungsverfahren.

Beim LZW-Verfahren werden häufig auftretende Sequenzen unter einem Index in einer Tabelle gespeichert. Dieser Index nimmt in der gesamten Datei den Platz der Sequenz ein. Da der Index viel weniger Speicherplatz beansprucht als die Sequenz, ist die Datei nach der Komprimierung kleiner. Eine so komprimierte Datei kann mittels LZW Algorithmus wieder vollständig rekonstruiert werden.

(Al|go|rith|mus)
(nach einem bestimmten Schema ablaufende Verarbeitungsvorschrift)

Die LZW Komprimierung ist am effektivsten, wenn die mit einem Index codierte Sequenz häufig auftritt.

Beispiel: LZW - Komprimierung

Der obere Bildausschnitt besteht aus verschieden farbigen Pixeln. Im RGB-Modus kann jedes Pixel einen von 16,7 Mio. Farbtönen annehmen und belegt somit 24 bit Speicherplatz. Nach dem LZW-Algorithmus werden nun Pixel-Sequenzen gesucht und mit einem Index in einer Tabelle gespeichert.

Der Index besteht aus Zeichen der ASCII-Tabelle. Ein ASCII-Zeichen benötigt nur 8 bit Speicherbedarf!

LZW Tabellenindex

Sequenz	bit	Index	bit
	24	I1	16
	48	I2	16
	72	I3	16
	48	I4	16
	24	I5	16
	48	I6	16
	24	I7	16
	48	I8	16
	48	I9	16

Vergleicht man die bits der Pixelsequenzen mit den bis der Indizes, erkennt man leicht, dass eine Speicherplatzreduktion möglich ist.

Diese Tabelle stellt nur ein theoretisches Beispiel dar. Der echte LZW-Algorithmus ist um einiges komplizierter. Aber wir sind ja auch keine Mathematiker.

Das unkomprimierte Bild hat eine Größe von 5 x 21 = 105 Pixel.

105 Pixel x 24 bit (RGB) = 2520 bit = 315 Byte.

Die komprimierte Form besteht aus 9 zusammengefassten Folgen, welche 52 Sequenzen ergeben.

Jede Sequenz wurde mit einem 2-stelligen ASCII-Index codiert. Dieser Index hat eine Größe von 16 bit.

52 Sequenzen x 16 bit = 832 bit = 104 Byte.

Bereits diese einfache Form des LZW Algorithmus erreicht eine Kompression um 67%. Der LZW-Algorithmus wird zum Erzeugen von GIF Bildern und bei der Datenübertragung in Modems angewendet. Optional kommt er auch bei TIFF Bildern in fragen. Bei der Dekomprimierung wird jedem Index, die entsprechende Pixelsequenz wieder zugeordnet und man erhält die Ausgangsdatei ohne Datenverlust.

RLE - Runlength Encoding

RLE ist ein verlustfreies Kompressionsverfahren und beruht darauf eine Folge von gleichen Zeichen / Pixel durch zwei Werte (Anzahl und Zeichen) verkürzt darzustellen. Dazu ist im Gegensatz zu LZW keine Tabelle notwendig.

RLE ist nur dann besonders effektiv, wenn in der zu komprimierenden Datei längere Folgen ein und des selben Zeichens vorkommen.

Dies ist z.B. bei Bitmaps oder Grafiken mit großen farbigen Flächen der Fall.

Bei einer entsprechenden Datei werden zeilenweise alle Zeichen oder Pixel gezählt, die zusammenhängend einen Wert haben. Diese Anzahl wird als 8 bit ASCII Zeichen gespeichert. In einem Bitmap wird jedes Pixel mit nur 1 bit gespeichert. Entwerder ist es schwarz oder weiß.

Daher ist die RLE Kompimierung in Bitmaps nur bei Folgen von min. 9 Pixel oder mehr sinnvoll. 9 Pixel benötigen 9 bit. RLE komprimiert werden 8 bit (ASCII-Zeichen) für die Anzahl und 1 bit für den Farbwert der Pixel gespeichert. Macht zusammen auch 9 bit.

Bei kleineren Folgen wird die Datei sogar größer!

Beispiel - Bitmap

Format 42x20 Pixel mit 1 bit/Pixel.
Speicherplatz = 840 bit .

Das 0 bit steht für weiße Pixel.
Das 1 bit steht für schwarze Pixel.

Die Zahl davor bezeichtet die Anzahl der Pixel und wird als 8 bit ASCII codiert.

420 = 9 bit
25011160 = 27 bit
25021150 = 27 bit
25031140 = 27 bit
25041130 = 27 bit
25051120 = 27 bit
25061110 = 27 bit
30291100 = 27 bit
3030190 = 27 bit
3031180 = 27 bit
3031180 = 27 bit
3030190 = 27 bit
30291100 = 27 bit
25061110 = 27 bit
25051120 = 27 bit
25041130 = 27 bit
25031140 = 27 bit
25021150 = 27 bit
25011160 = 27 bit
420 = 9 bit

Speicherplatz RLE komprimiert = 504 bit

Durch die RLE Komprimierung verringert sich in diesem Beispiel die Dateigröße von 840 bit auf 504 bit. Das ist eine Komprimierung um 40%.

Negativ-Beispiel - Bitmap

Das unkomprimierte Bild hat eine Größe von 5 x 21 = 105 Pixel.

105 Pixel x 1 bit/Pixel = 105 bit.

51104110411051 = 63 bit
201130114011601120 = 81 bit
201130312041301120 = 81 bit
20113011701111301120 = 90 bit
201130411041301120 = 81 bit

Die RLE komprimierte Datei wird um über 377% auf 396 bit künstlich vergrößert.

In diesem Bsp. ist die RLE Komprimierung nicht sinnvoll, da es nicht genügend große Flächen gleicher Pixel gibt.

Beispiel - CMYK Grafik

In CMYK Grafiken hat jedes Pixel eine Farbtiefe von 32 bit. Bereits ab einer Folge von 2 gleichen Pixeln erreicht man mit RLE eine Komprimierung.

6 x 32 bit = 192 bit

RLE komprimiert:

2x2x2x = 120 bit

8 bit + 32 bit + 8 bit + 32 bit + 8 bit + 32 bit = 120 bit

Huffman-Kodierung

Dieses Verfahren, benannt nach dem amerikanischen Mathematiker David Huffman, ermittelt wie häufig jedes Zeichen / Pixel in einer Datei vorkommt. Die häufigsten Zeichen / Pixel werden mit der kleinsten bit-Sequenz kodiert, die weniger häufig auftretenden mit längeren bit-Sequenzen. Dazu wird eine Tabelle verwendet.

Dieses Verfahren wird als Entropie Kodierung bezeichnet.

Das Verfahren ähnelt dem Morsen, wo der im Deutschen am häufigsten verwendeten Buchstaben "e" das kürzeste Morsezeichen "·" besitzt.

Beispiel - Huffman Kodierung

Nehmen wir mal die zuvor mit LZW komprimierte Datei mit einer Größe von 832 bit.

Nach der Huffman Methode ist es möglich die Häuffigkeit zu ermitteln und die einzelnen Sequenzen kürzer zu kodieren.

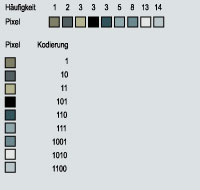
Die nach Huffman kodierte Datei hat nun eine Größe von 26 bit.

Mit Huffman lassen sich beliebige Daten komprimieren, da immer Zeichen verschiedener Häufigkeit vorkommen.

Erstellt am 22. April 2008